La distribución normal se puede utilizar como una aproximación de distribuciones discretas, en particular cuando el tamaño de la muestra "n" tiende a infinito, p y q cercanos a 0.5 se puede aproximar a la distribución binomial, con resultados altamente satisfactorios.
Sea X una variable aleatoria con distribución binomial, si n es grande, 0 < p < 1, la distribución binomial se puede aproximar a la distribución normal con media µ= np y varianza σ²= npq
.
lo que nos permite el cálculo de la siguiente probabilidad:
Sea X una variable aleatoria con distribución binomial, si n es grande, 0 < p < 1, la distribución binomial se puede aproximar a la distribución normal con media µ= np y varianza σ²= npq
.
La distribución normal tiene como fdp,
Por lo tanto la distribución aproximada estará dada por:
El teorema de Moivre (1.756) permite realizar esta aproximación considerando p=q=1/2 que las variables aleatorias sigan una distribución binomial con: . Este teorema fue generalizado posteriormente por Laplace en 1.810 para distribuciones no simétricas p≠q .
Vimos que la variable aleatoria binomial era el número de éxitos que tienen lugar cuando se realizan n repeticiones independientes de un experimento o prueba de Bernoulli. La variable aleatoria x puede escribirse como la suma de n variables aleatorias de Bernoulli:
media 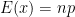
desviación típica 
entonces, cuando n → ∞ la variable aleatoria:
es decir: x→N(np,npq)
En la práctica, decir que n es lo suficientemente grande, se traduce en:
Lo que se hace es aproximar una distribución discreta, como es la binomial, a una distribución normal que es continua, y ya que en el caso continuo la probabilidad o masa asociada a un valor concreto de la variable aleatoria es nulo, tendremos que utilizar la corrección de continuidad de Fisher para calcular la probabilidad deseada:
Probabilidad en B (n,p) Corrección de continuidad
P(X=x) P(x-1/2<X<x+1/2)
P(X<X<b) P(a-1/2<x<b+1/2)
P(X<x) P(X<x+1/2)
PX>x) P(X>x-1/2)
A continuación te damos un ejercicio a resolver y las respuestas a las que hay que llegar:
En una estadistica que realizo una Empresa de Celulares, encontro que 70% de los celulares robados no fueron recuperados. Se reportaron en un mes 200 robos, ¿Cúal es la probabilidad de que no se recuperen, a) a lo mas 145 de estos celulares?, b) entre 130 y 155 de estos celulares inclusive?, c) más de 150 de estos celulares, d) exactamente 128 de estos celulares?
Solución
a)
p= 0.7
q= 0.3
n= 200


